정렬

정렬 알고리즘

n개의 데이터가 입력으로 주어졌을 때,
특정한 기준에 따라 해당하는 데이터에 순서대로 열거하는 것
데이터를 정렬하는 경우 효율적인 ‘탐색’이 가능해진다

안정성

정렬할 데이터(원본)의 ‘반복’되는 요소를 받은 그대로 처리하는 경우는 ‘안정 정렬’ 이라 한다.
반대로 뒤섞일 가능성이 있다면 ‘불안정 정렬’이라 한다.

알고리즘의 종류

정렬 알고리즘의 종류는 다양하나,
여기서는 아래의 알고리즘들을 소개해볼까 한다

• 삽입정렬
• 퀵정렬 (Quick sort)
• 병합정렬 (merge sort)
• 힙정렬 (heap sort)
• 쉘정렬 (shell sort)

삽입정렬

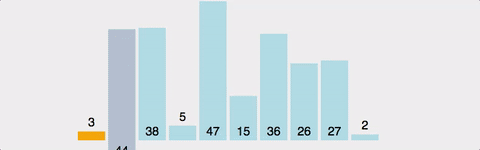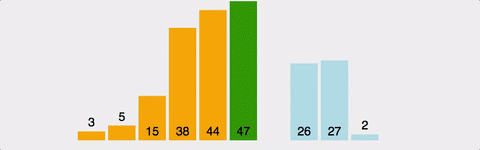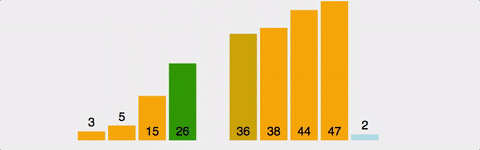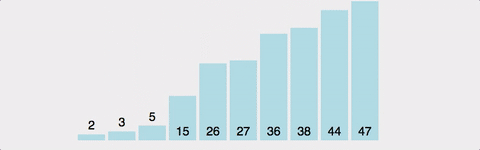
k번째 원소를 1~(k-1)의 원소와 비교하여
적절한 위치에 ‘삽입’한 뒤, 그 뒤의 원소들을 뒤로 미루는 정렬이며 ‘안정 정렬’이다.

시간 복잡도 (평균) : O(n^2)
시간 복잡도 (최선) : O(n) (이미 정렬이 되어 있는 경우)

‘이미 어느정도 정렬된’ 배열에서 사용하기 유용한 알고리즘
(해당 부분에 한하여 O(n)에 해당하는 복잡도를 가지게 되므로)

구현 예시(Python)

  def Inser_Sort(lst :list)->None:
    lstLength = len(lst)
    # 삽입정렬
    # n번째 요소가 n-1보다 작은 경우
    # 해당 위치에 삽입해준다
    for i in range(lstLength):
        for j in range(i):
            if lst[i] < lst[j]:
                a = lst[i]
                lst.pop(i)
                lst.insert(j,a)

퀵 정렬

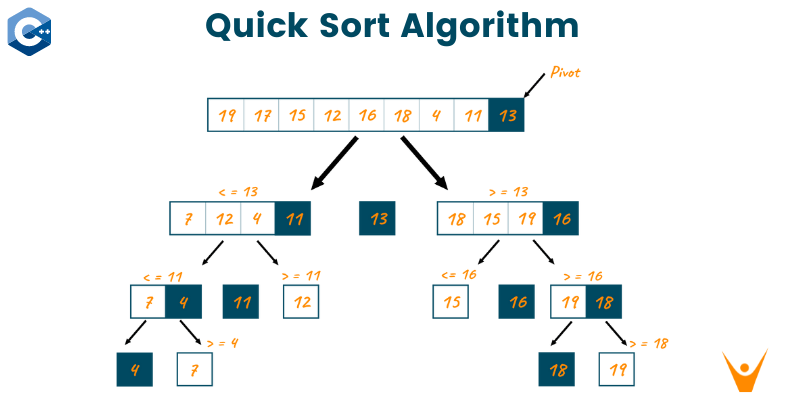
데이터에서 임의의 값을 기준값(pivot)으로 정한뒤, 2개의 집합으로 나눈다.
기준값보다 작은 쪽과 큰 쪽으로 나눈뒤,
각각의 집합에서 기준값을 만들고 다시 위의 내용을 실행한다.
더 이상 집합을 나눌 수 없을때까지 반복하면 된다
퀵 정렬은 ‘불안정 정렬’이기에,
정렬 이후의 원본과의 ‘반복 요소’의 순서가 변할 수 있는 점을 유의해야 한다

시간 복잡도 (평균) : O(n log n)
시간 복잡도 (최악) : O(n^2)
(배열이 이미 정렬되어 있는 상황에서 사용하거나,
임의의 기준값을 선택할 때, 최솟값, 최댓값을 반복적으로 선택하는 경우 발생 가능)

퀵정렬 진행방식

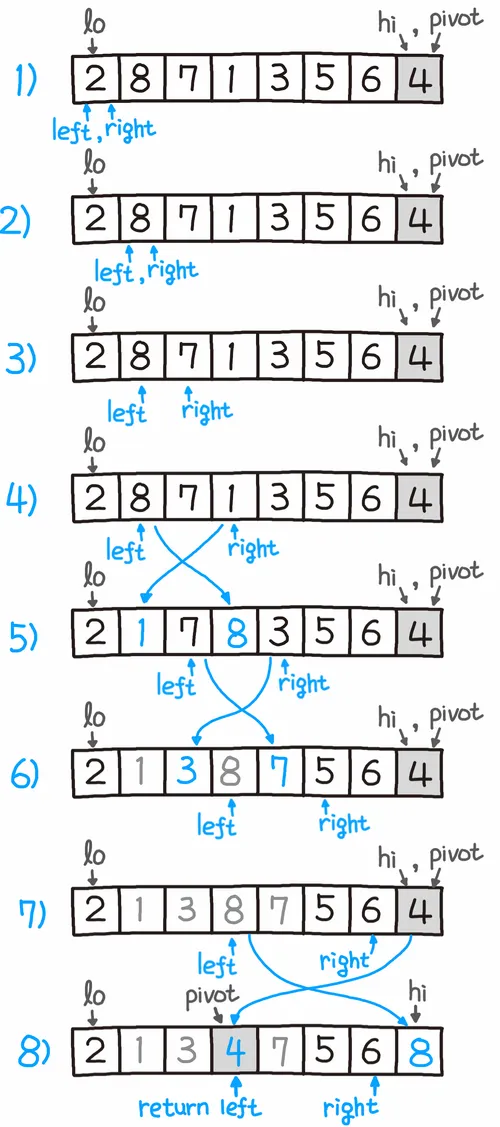
가장 많이 사용되는 정렬 알고리즘?

퀵 정렬의 루프 방식이 대부분의 컴퓨터 아키텍처에서 효율적으로 동작하게 설계되어 있다
(메모리 참조가 지역화되어 있기때문에 CPU 캐시의 히트율이 높아지기 때문)
데이터가, 점점 좁은 범위에서 서로 교환되며,
이는 캐시를 통해 해당 데이터를 가져올 확률이 올라가게 된다!
따라서 퀵 정렬은 같은 시간 복잡도를 가졌더라도, 다른 정렬에 비하여 캐쉬의 도움을 받을 가능성이 높다!

(지역화 : CPU가 짧은 시간 내에 일정 구간의 메모리 영역을 반복적으로 엑세스하는 경향)

구현 예시(Python)

  def quickSort(left : int,right : int,lst :list)->None:
    # pivot은 가장 맨 끝으로 잡을 예정
    # 왼쪽 index(left) 오른쪽 index(right)(pivot)
    # 왼쪽 진행하면서 lst[left + 1]이 pivot보다 작다면 lst[left]와 swap
    # (중간에 pivot보다 교환 못하는 것을 발견해도 내버려둔다)
    # 이제 왼쪽과 오른쪽을 교체하고(swap)
    # quickSort를 (0 pivotPos -1), (pivotPos + 1 , length) 로 각각 호출
    # 이건 오른쪽을 pivot으로 잡은 경우

    if left >= right:
        return

    pivot = lst[right]      # 가장 오른쪽의 값을 pivot으로
    changeIndex = left - 1  # 왼쪽에서 넘어가면서 값을 바꿔줄 인덱스 번호

    for i in range(left, right):
        if lst[i] < pivot:
            changeIndex += 1
            lst[changeIndex],lst[i] = lst[i], lst[changeIndex]

    pivotPos = changeIndex + 1
    lst[pivotPos],lst[right] = lst[right],lst[pivotPos]

    quickSort(left, pivotPos - 1,lst)
    quickSort(pivotPos + 1,right,lst)

def QuickSort(lst : list)->None : 
    quickSort(0,len(lst)-1,lst)

병합정렬

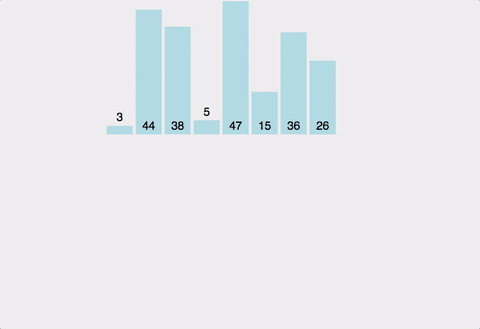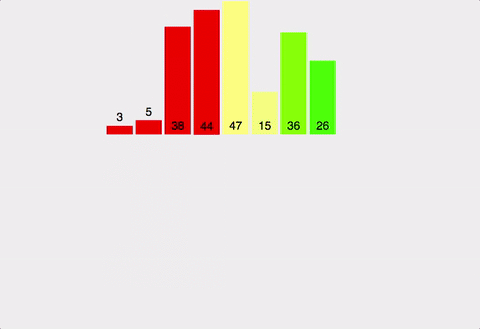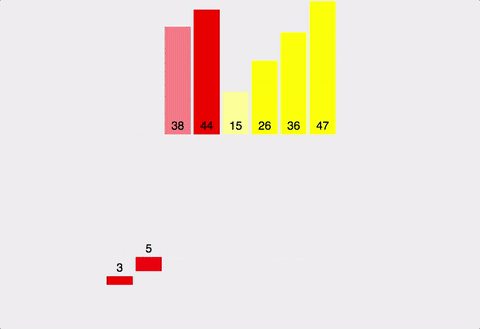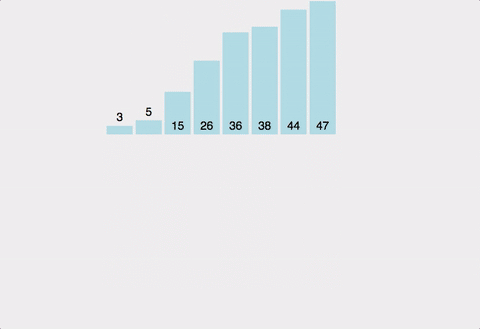
병합 정렬은 ‘분할 -> 정렬 -> 결합’의 순서로 이루어지는 정렬 알고리즘이다.

• 분할

  데이터 배열을 2개 이상의 부분 배열로 ‘분할’한다

• 정렬

  부분 배열 내부 요소들끼리 ‘정렬’한다

• 결합

  해당하는 부분 배열들을 ‘결합’ 한다
  이후 ‘정렬’ -> ‘결합’을 반복하여 데이터 배열 전체가 정렬된다

시간 복잡도 (평균,최선,최악) : O(n log n)
항상 일정한 시간 복잡도를 유지하고 ‘안정 정렬’인 특징이 있으나,
정렬을 위한 추가적인 배열 공간을 사용하는 점 또한 유의해야 한다.

구현 예시(Python)

  def mergeSort(lst:MutableSequence)->None:
    n = len(lst)
    buff = [None] * n
    _merge_Sort_Recur(lst,buff,0,n-1)
    del buff

def _merge_Sort_Recur(lst:MutableSequence,buff :MutableSequence,left :int,right:int)->None:
    if left < right:
        mid = (left+right) // 2

        _merge_Sort_Recur(lst,buff,left,mid)     # 배열의 앞 부분
        _merge_Sort_Recur(lst,buff,mid+1,right)  # 배열의 뒷 부분

        # buffs index
        buffHalfs = 0 # buff의 최댓값을 가리키는 인덱스
        buffIndex = 0 # buff(뒷부분 배열)을 가리키는 인덱스

        # lst index       
        i = left    # lst의 뒷부분을 가리키는 용도의 인덱스(처음에 buffHalf와 같이 올려준다)
        k = left    # lst의 앞부분을 가리키는 용도의 인덱스(점점 올라가며 삽입할 위치를 찾음)

        # 배열의 앞부분(lst[left]~lst[mid])을
        # buff[0]~buff[mid - left] 로 복사
        while i <= mid:
            buff[buffHalfs] = lst[i]
            i +=1
            buffHalfs +=1
        # 종료시점의 buffHalfs값은 mid - left + 1
        
        # 배열의 뒷 부분(lst[mid + 1]~lst[right])과
        # buff로 복사한 배열의 앞부분 buffHalfs 개를
        # 병합한 결과를 lst에 저장
        while i<=right and buffIndex < buffHalfs:
            if buff[buffIndex] <= lst[i]: # lst의 뒷부분 요소가 buff(현재 배열 앞부분) 보다 작은 경우
                lst[k] = buff[buffIndex] # buff 요소를 k에 넣어준다
                buffIndex+=1
            else:
                lst[k] = lst[i] # 그게 아니면 뒷부분 값을 넣어주고, i를 올린다
                i +=1
            k +=1

        # buff에 남아있는 원소를 배열 lst에 복사하기
        while buffIndex < buffHalfs:
            lst[k] = buff[buffIndex]
            k+=1
            buffIndex+=1

        # 요점은 배열의 앞부분과 뒷부분을 따로 쓴다는 점
        # 또한 buff를 처음 생성한뒤 해당 공간을 다 쓴후 해제

힙정렬

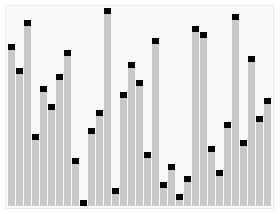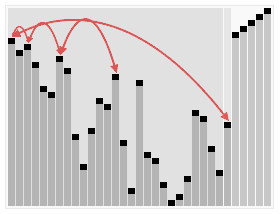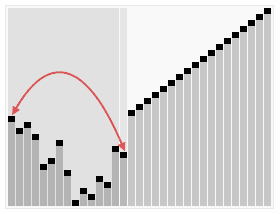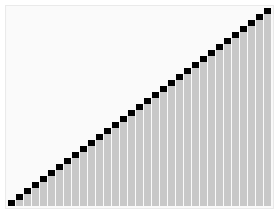
‘힙 트리’를 구성해 정렬을 하는 방법
배열 요소들로 ‘완전 이진 트리’를 구현하고,
(오름차순,내림차순에 따라 각각 최소 힙, 최대 힙으로 구성)
이후 힙에서 하나씩 요소를 꺼내어 배열의 뒤부터 저장
(요소가 하나 줄어들면 힙트리가 다시 ‘정렬’된다)

시간 복잡도 (평균,최선,최악) : O(n log n)
항상 일정한 시간 복잡도를 유지하는 점이 특징
가장 특징적(최댓,최소)인 데이터 몇 개가 필요할 때 유용한 알고리즘
(‘힙 트리’의 앞부분만 빼내 쓸 수 있으므로)

쉘정렬

배열의 요소들을 각각 h(간격)씩 떨어진 요소끼리 정렬한 후,
h를 줄여나가며 결과적으로 배열 전체를 정렬

정렬 횟수는 많지만, ‘전체적’으로
원소의 이동 횟수가 줄어들어
효과적인 알고리즘이다
(퀵 정렬이 고안되기 전 가장 빠른 정렬이라는 말이…)

다만 ‘간격’을 잘못 잡는 경우,
효율이 굉장히 떨어지게 된다
보통 h//3 의 간격을 사용

예시 코드 (Python)

def shell_sort(a:MutableSequence)->None:
    n = len(a)
    h = 1

    # 원소를 뒤섞이게 하려고 배수가 아니게 설정
    while h < n //9:
        h = h * 3 + 1

    while h > 0:
        for i in range(h,n):
            j = i - h
            tmp = a[i]
            while j >=0 and a[j] > tmp: # h 만큼
                a[j+h] = a[j]
                j -= h
            a[j+h] = tmp
        h //= 3

GIF 출처

[GIF 이미지 출처 : J Stroy ]https://aiday.tistory.com/53