깊이 우선, 너비 우선 탐색

DFS vs BFS

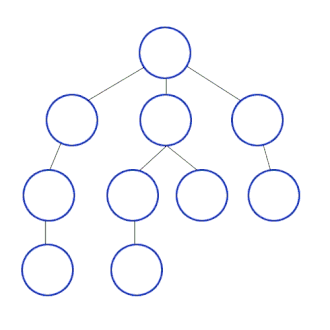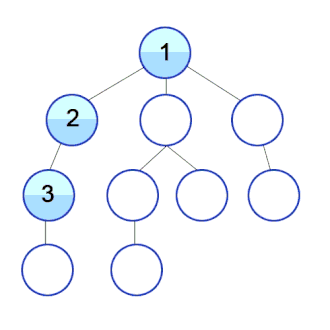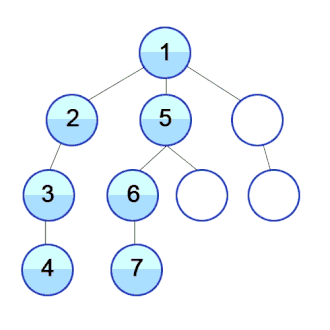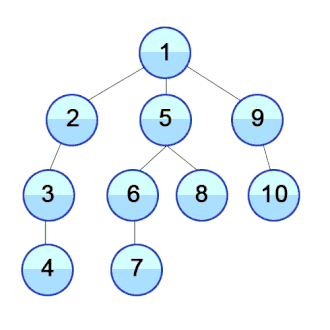
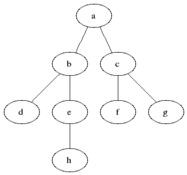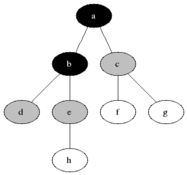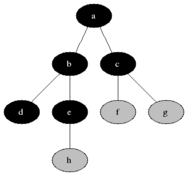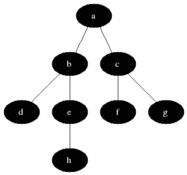
‘Tree’ 속에 저장된 것 처럼 보이는 ‘Data’를
찾고 있을 때 사용하는 ‘방문순서’ 규칙

‘각 노드’에서 실행할 수 있는 ‘알고리즘’이 필요!

DFS : 먼저 하나를 타고 쭈~욱 깊이 내려가기
BFS : 모든 ‘자식’노드를 보면서 없으면 다음 노드 내려가기

DFS

‘한 우물 깊이 파기’

‘중위’ 순회와 매우 비슷하기에 쉽게 구현 가능
(‘스택’을 이용하여 비재귀적으로도 구현 가능)

예시코드 python (비재귀)

    def searchDFS(node : Node):
        stack = deque()

        stack.append(node)

        while stack:
          next = stack.pop()

          print(next.data)

          # 이진 트리가 아닌 경우는 for로 자식들 돌린다
          if next.left:
            stack.append(next.left)
          if next.right:
            stack.append(next.right)
  

(참고로 stack 이 아닌 queue인 경우, 바로 BFS가 된다)

• 장점
  

  구현이 직관적 (재귀/stack)
  BFS보다 메모리 사용량 적음
  (언제나 그런것은 아니지만, 확률 높음)
  캐시 메모리 친화적
  (해당 데이터와 ‘인접한 자식’ 데이터를 보기에
  캐시 적중률이 높아짐)
  병렬처리에 적합
  (반복적으로 ‘분리’가 가능)
  

• 단점
  

  최단 경로 찾기에는 적합하지 않음
  (같거나 비슷한 값이 더 낮은 깊이에 존재하는데
  더 깊이 있는 데이터를 가져올 수 있음)
  

BFS

‘여러 우물 동시에 같이 파기’

현재 깊이의 이웃 노드들을 우선적으로 방문하기
-> 어느 한 가지만 ‘깊이 보지 않음’
-> 이미 ‘현재 노드’보다 ‘얕은 깊이’를 가진 녀석들은
탐색했다는 가정이 가능함

• 따라서 최단 경로 찾기에 적합함
  
  

예시코드 python

    def searchDFS(node : Node):
        queue = deque()

        queue.append(node)

        while queue:
          next = queue.popLeft()

          print(next.data)

          # 이진 트리가 아닌 경우는 for로 자식들 돌린다
          if next.left:
            queue.append(next.left)
          if next.right:
            queue.append(next.right)
  

• 장점
  

  언제나 최소 깊이의 결과를 찾음
  깊이가 ‘무한’ 인 tree 에도 이용 가능
  (그렇다고 너무 과신하진 말것)
  MST를 찾는데 유용하게 사용 가능
  

• 단점
  

  메모리 사용량이 높아질 가능성