그래프

그래프의 정의

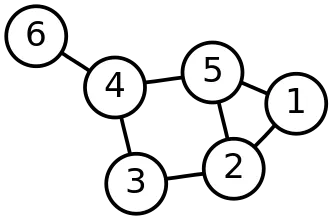
‘데이터’를 잘 정리하는 방법

• 데이터: 노드(Node), 정점(Vertex), 꼭짓점(Point)
• ‘잘 정리’ : ‘데이터 간의 관계’
  -> 변(Edge), 간선 등
  => 관계에 ‘방향성’(Arc)가
  존재 가능!

‘데이터와 그 간의 관계’를 설명!

서로 연관된 데이터의 집합이며,
‘복잡한’ 문제를 구현하기 위해
적절한 자료구조

• 차수?
  

  하나의 노드(Node)에
  연결된 다른 간선(Edge)의 수

• 순환(loop)?
  

  노드의 간선이 ‘자신’을
  가리키는 것
  그래프 전체적으로는
  노드가 자신으로 ‘돌아올
  수 있느냐’의 의미이다

그래프의 종류

• 무방향 그래프
  

  변에 특별한 방향(arc)가 없음
  A - B
  A와 B는 서로를 가리키고 있다고
  인식이 가능하다
  

  여담으로 모든 노드가
  서로를 가리키고 있다면
  ‘간선’의 총 개수는
  

        E = n(n-1) / 2
  

• 방향 그래프
  

  변이 하나의 방향만 가리킴
  A -> B
  A’가’ B를 가리키는 상황
  B는 A를 가리키지 않음
  

• 순환 그래프
  

  노드에서 다른 간선을 통해
  넘어가도 다시 돌아올 수 있는
  그래프

• 비순환 그래프
  

  모든 그래프에서
  하나의 노드에서 떠난 것은
  다시 그 노드로 돌아가지 않음
  

• 가중 그래프
  

  각 변의 관계 정도가 다름
  (ex : 비용, 시간)
  각 간선의 값이 다를 수 있음

• 비가중 그래프
  

  모든 간선이 동일한 의미를 가짐
  각 간선의 값이 같음
  

  (트리도 위 종류의 조합으로)
  (설명이 가능하다)

그래프의 표현

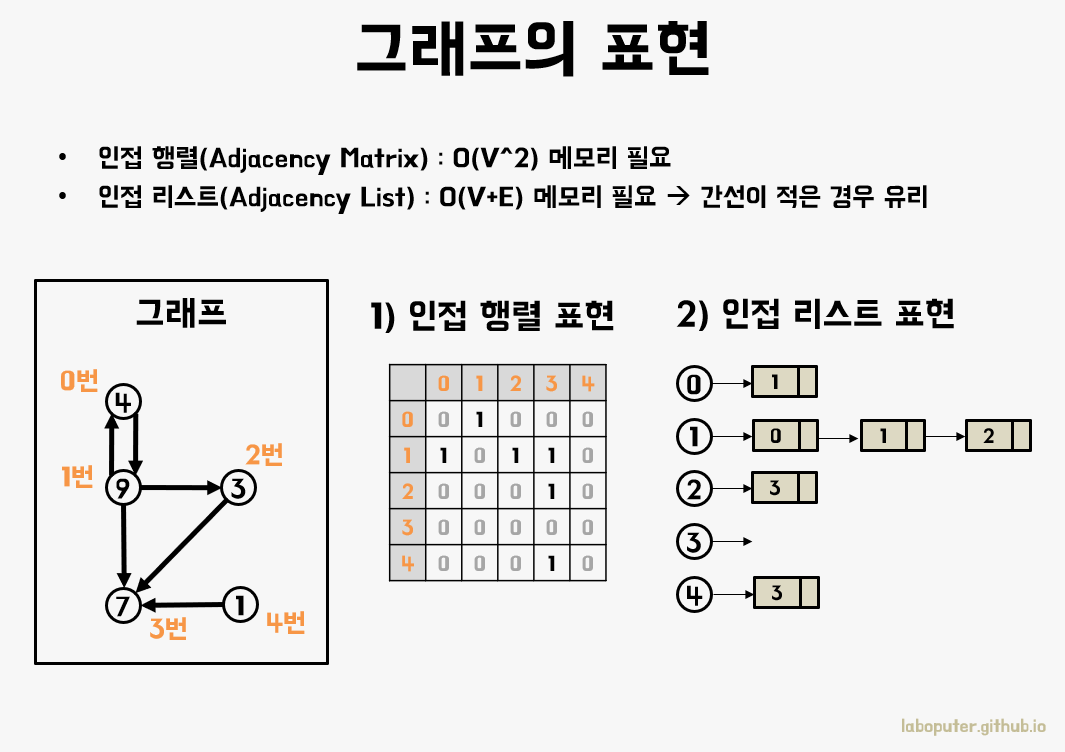
주로 코드로 ‘그래프’를 표현하는 방식

• 인접 행렬(Adjacency Matrix)
  

  2차원 배열로 정점 간의 간선을 표현
  (간선이 있다면 1,
  없으면 0)
  
  

  장점 : 구현이 쉽다!
  간선 제거의 시간 복잡도가 O(1)
  간선 탐색의 시간 복잡도가 O(1)
  
  

  단점 : O(노드**2) 의 공간복잡도
  언제나 같은 공간 사용
  (간선이 적든 많든)
  인접 행렬 생성의 시간복잡도 O(N^2)
  동적인 구조 변경의 어려움
  

• 인접 리스트(Adjacency List)
  

  정점의 개수만큼 리스트를 만들어
  각각의 정점 리스트에 간선 추가
  (연결 리스트 N개를 배열에 저장)
  (동적 배열도 사용가능)
  
  

  장점 : 공간 적게 사용
  (O(노드 + 간선),
  단 최악은 O(N^2))
  노드 삽입 삭제 빠름(연결 리스트)
  
  

  단점 : 간선 탐색이 다소 느림
  (노드 A -> 노드 B 의 ‘간선’ 검색이 O(V))
  두 노드의 ‘연결’ 여부를 파악하는데는
  ‘인접 행렬’보다 느림