최단 경로 알고리듬

8 분 소요

최단 경로 문제

그래프 이론에서 ‘가장 짧은 경로’에서
두 꼭짓점을 찾는 문제

이 해결을 위한 알고리즘으로는

다익스트라 알고리듬
벨먼-포드 알고리듬
A* 탐색 알고리듬
플로이드 - 와셜 알고리듬

이 존재한다

다익스트라 알고리듬

Scc

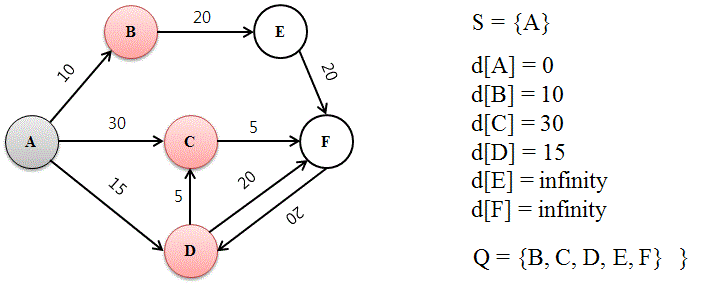
두 노드 사이의 ‘최단 경로’를 찾음
그래프가 방대한 경우에도 사용하기 충분히 빠름
간선의 ‘가중치’가 ‘음수’인 경우 제대로 동작하지 않음
(한 번 방문한 노드를 ‘다시’ 방문 안하기에
가중치가 ‘양수’인 경우에만을 가정)
(이 경우는 벨만-포드 알고리듬 이용)

실제로 지도/내비게이션, IP 라우팅 등으로 많이 사용

‘정렬’이 필요하기에(최단 거리 선택을 위함)
그에 따라, 정렬을 하거나 ‘우선순위 큐’ 자료구조를 이용한다

알고리듬 적용 방식
1. 아직 방문 안한 노드 중 ‘가장 가까운 노드’(n)를 선택
2. n의 이웃 노드 m으로의 여행거리를 계산(n거리와 n->m 거리)
3. 이 결과가 m의 ‘기존 거리’보다 가까우면 m의 거리를 업데이트 -> 모든 노드를 방문하면 ‘최단 거리’를 찾음
  => 모든 노드를 거쳐 온 경로 중 최솟값을 취했기 때문
탐욕(Greedy)스러운 알고리듬

그리디는 나중에 따로 포스팅,
기본 개념은 ‘현 시점의 최선의 선택’
또한 ‘동적 계획법’(Dynamic Programming,DP)이기도 하다

기존의 경로 거리를 업데이트 하며 이를 재활용한다
(‘최단경로’는 ‘여러 개’의 ‘최단경로’가 모여 만들어질 수 있음
따라서 ‘분할’이 가능한 문제)

다익스트라의 조금 더 상세한 적용 방식

아직 방문 안한 노드 중 가장 거리 값이 작은 노드 ‘n’ 선택
n의 ‘미방문’ 이웃 m으로 가는 더 짧은 경로가 있다면 업데이트
min(현재까지 아는 m의 거리,
현재까지 아는 n의 거리 + n->m 거리)
다음 조건 중 하나를 만족할때까지 1~2 반복
- 모든 노드를 방문
- n이 목적지
목적지까지의 거리/경로 반환

정확히는 ‘간선’의 가중치를 업데이트 하는 것이 아니라
‘노드’에 도착하는 최소 거리를 업데이트 한다
(그렇기에 처음에는 ‘노드’의 거리를 INT_MAX 같은 걸로 초기화)

이후 업데이트 한 뒤,
추가적으로 ‘가장 짧은’ 거리만 돌도록 순회하며,
경로와 최소 길이를 반환 가능하다

다익스트라의 ‘시간 복잡도

보통은 ‘인접 리스트’를 사용한다고 가정
(실제로 ‘많은 데이터’가 있을 때, ‘인접 배열’은 너무
많은 메모리를 잡아 먹음)

방문하는 노드 수(= 알고리즘 실행 횟수) : N
(모든 노드를 방문하므로 최소 N번 방문한다) 최소 거리 노드 선택 : 약 N /2 = N
간선 이동 : E
=> 따라서 O(N^2 + E) => O(N^2)
다만 ‘최소 거리 노드 선택’ 알고리즘을 개선하여
더 빠르게 가능
최대 O((N+E) log N) 까지 개선할 수 있다 한다
(E Log N) : 거리값 업데이트 시, ‘우선순위 큐’의
거리값도 업데이트 되어야 하기에 ‘리밸런싱’의 비용

우선순위 큐 말고도 ‘힙’ 등을 사용해서 구현도 가능

다익스트라 코드 예시(백준 1916)

heapq(우선순위 큐) 를 사용하였으며, 그렇지 않은 경우는
cost 에 따른 ‘정렬’을 해야한다

import sys
import math
import heapq

cityNum = int(sys.stdin.readline().strip())
busNum = int(sys.stdin.readline().strip())
buses = [[] for _ in range(cityNum)]

for i in range(busNum):
    start,to,cost = map(int,sys.stdin.readline().split())
    buses[start-1].append([to - 1,cost]) # buses[start] 에 목적지와 cost를 담아둔다


start,to = map(int,sys.stdin.readline().split())
start -= 1
to -= 1

def dijkstra(start,to,buses):
    # 각 도시간의 거리 (시작점 기준)
    distance = [math.inf] * cityNum
    distance[start] = 0 # 시작점은 0으로

    # queue 대신 heapq 를 사용하면 다익스트라
    minheap = []

    heapq.heappush(minheap,(0,start))

    while minheap:
        curr_cost,city = heapq.heappop(minheap)

        for next_city,next_cost in buses[city]:
            new_cost = distance[city] + next_cost

            # 새로운 비용이 기존 비용보다 작다면 업데이트 후, 힙에 추가
            if new_cost < distance[next_city]:
                distance[next_city] = new_cost
                heapq.heappush(minheap,(new_cost,next_city))

    return distance[to]
  
print(dijkstra(start,to,buses))

벨먼 - 포드 알고리듬

가중치가 있는 ‘방향’ 그래프에서
‘최단 경로’를 찾는 알고리즘 중 하나

‘음수 가중치’ 간선이 있는 그래프에서도
동작하며, ‘음수 가중치 사이클’을 감지할
수 있다.
(그래프의 시작점에서, 특정 정점까지 도달하기
위해 거쳐 가는 최대 간선수가 v - 1 개 이기에
V번쨰 간선에 도착한 순간, 사이클의 존재를
파악할 수 있다)

동작 원리
1. 시작 정점 결정
2. 시작 정점에서 다른 정점까지의 거리를 초기화
  (INT_MAX 등)
  (시작 정점 의 거리는 0으로 시작)
3. 현재 정점에서 모든 인접 정점들을
  탐색하며, 기존에 저장되어 있는 거리
  (distance[a])보다 해당 정점을 ‘경유’하여
  도달하는 거리가 더 짧은 경유 짧은 쪽으로 갱신
4. 3번의 과정을 v-1번 반복
5. 4번 이후 거리가 다시 갱신된다면 ‘음수 사이클’
  존재

벨만-포드 알고리즘 코드 예시(Python)

함수만 구현한 의사코드

import math

# 벨만 포드 알고리즘
# 1. 음수 가중치가 있는 그래프에서
# 시작 정점에서 다른 정점까지의 최단 거리를 구할 수 있음
# 2. 음수 사이클의 존재를 알 수 있음

# 1. 노드별 거리 초기화
# 2. 연결된 모든 간선 탐색하여 노드별 거리 업데이트
# (총 간선의 개수는 n-1개 이므로, 최대 n-1까지)
# 3. 2의 방식을 한번 더 수행하고
# 거리가 '업데이트' 된 경우, '음수 사이클'이 존재한다고 판정
# 그렇지 않다면 시작 - 목표 거리 반환하기

# 시간 복잡도(최악)는 O(VE) (모든 간선에 대하여 반복하며, 각 노드를 검사)

def bellman_fod(graph,dest,nNum):
    distance = [math.inf] * nNum
    distance[dest] = 0

    for i in range(nNum - 1):
        for st, to, cost in graph:
            if (distance[st] != math.inf and            # st가 아직 방문되지 않음
                 distance[st] + cost < distance[to]):   # 다음 목적지보다 st 경유해서 가는게 더 작다
                    distance[to] = distance[st] + cost
    
    for st, to, cost in graph:
         if (distance[st] != math.inf and
                 distance[st] + cost < distance[to]): # 음의 사이클이 존재하는 상황이다
                    return -1

    
    for i in range(nNum -1):
          if distance[i] != math.inf:
            print(f'{i} 노드부터 {dest}까지의 거리 : {distance[i]}')
          else:
            print(f'{i} 노드부터 {dest}까지 도달할 수 없어요!')

    return True

A* 알고리듬

다익스트라는 충분히 훌륭한 알고리즘
시간 복잡도도 훌륭!

다만 실제로는 워낙 많은 노드를 뒤지기에
실행 속도가 그렇게 빠르진 않음
~~(n log n 이지만 n이 크게 들어오는 느낌)~~

이러한 단점을 ‘보완’하여 만들어진 알고리듬이
A*

다익스트라와 비슷한 개념의 알고리듬
하지만 불필요한 ‘평가’를 하지 않는다
(ex : 서울 -> 부산 가는데,
북쪽으로 가는 경로를 들리지 않음)

이를 위해, ‘다음 노드 선택’시 기준 노드 추가!
다익스트라는 ‘시작점’ -> ‘목적 노드’까지의
거리를 기준으로 삼지만,
A*는 ‘현재 노드’ -> ‘목적 노드’까지의 거리를
기준으로 삼는다!

다만 A*가 추가한 기준은 결정적이 아님
‘휴리스틱’하며, ‘근사치’ 에 가깝다
(Greedy 하기에, 최적해가 아닐 수 있음)

이렇게 ‘조건’을 보조해주는 함수에 따라서
A*의 성능이 달라진다

그러나,
‘대부분’의 경우, 다익스트라 보다 빠름
(데이터에 따라서 느릴수는 있음!)

A*의 2가지 노드 선택 기준

g(n) : 시작 노드부터 노드 N까지의 거리(실제값)
h(n) : n부터 목적지 노드까지의 거리(추정값)
f(n) : 시작 노드부터 목적지 노드까지의 거리(추정치)

f(n) = g(n) + h(n)

다음 노드 선택시,
다익스트라는 g(n)이 최소인 것을 선택하고
A*는 h(n)이 최소인 것을 선택한다

h(n)??

계속 목적지쪽의 노드를 우선적으로 선택해야 하기에
목적지에 가까울수록 h(n)이 작아야 한다
=> 따라서 ‘거리 계산 함수’로 표현되기도 한다
(모든 상황에서 최선인 것은 없으니)
(상황에 따라서 다양하게 선택한다)
(ex : 유클리드 거리, 맨해튼 거리)

구현시 특이점

최단 경로 후보 노드 집합 존재
해당 후보 선택시 최소 f(n)을 이용한다
같은 노드를 2번 이상 방문할 수 있음!
(다만 일반적으로는 재방문을 허용하지 않는 점은 유의)
A*가 중복 방문을 허용하는 이유?

다익스트라는 새로 방문하는 노드의 실제거리가
최소 (실제 거리인 g(n)만 사용)
다만 A*는 새로 방문하는 노드의 거리가
‘실제 거리’가 아니기에,
‘나중에’ 다른 경로를 반복함으로서
거리가 작아질 수 있음
휴리스틱 함수 (h(n)) 와
‘후보 노드 집합’에 사용하는 ‘자료구조’에 따라
시간 복잡도가 달라진다

A*의 세부 구현 과정

그래프의 모든 노드의 g(n)과 f(n)을 INF로
초기화
g(s) = 0, f(s) = h(s) (시작지점 초기화)
시작 노드 s를 후보 노드 집합에 추가
후보 노드 집합에서 f(n)이 가장 작은 노드를 제거
n의 각 이웃 m에 대해 시작점 -> n -> m이
더 짧은 경로인지 검사 후
g(m) = min(s->m,s->n->m)
이후, m을 후보 노드 집합에 추가
목적지에 도달하거나,
후보 노드 집합이 빌때까지 4~5 반복하기

A* 예시 코드 (Python)

휴리스틱으론 ‘맨해튼 거리’ 사용

import math
import heapq

# 노드
class Node:
    def __init__(self,parent = None, position = None) -> None:
        self.parent = parent
        self.position = position
        self.fValue = 0 # 시작지점부터 목적지의 추정 cost 합 (g + h)
        self.gValue = 0 # 시작 노드에서 현재노드까지의 총 cost 합 (실제 여기까지의 거리)
        self.hValue = 0 # 현재 노드에서 목적지까지의 추정 거리 (heuristic 이기에 틀릴 수 있음)
        
    def __eq__(self, other) -> bool:
        return self.position == other.position

# 휴리스틱
# 맨해튼 거리
def heuristic(node : Node,goal : Node):
    return abs(node.position[0] - goal.position[0]) +  abs(node.position[1] - goal.position[1])

def aStar(maze, start, end):
    # startNode와 endNode 초기화
    startNode = Node(None, start)
    endNode = Node(None, end)

    # openList, closedList 초기화
    openList = []       # 앞으로 볼 노드
    closedList = set()     # 이미 본 노드

    # openList : 우선순위 큐
    heapq.heappush(openList,startNode)

    # endNode를 찾을 때까지 실행
    while openList:

        # 현재 노드 지정
        currentNode = heapq.heappop(openList)

        # 현재 노드가 목적지면 current.position 추가하고
        # current의 부모로 이동
        if currentNode == endNode:
            path = []
            current = currentNode
            while current is not None:
                path.append(current.position)
                current = current.parent
            return path[::-1]  # reverse (뒤집어 줌으로서, 경로를 반환한다)
        
        # set에 더해주기
        closedList.add(currentNode)

        # 인접한 xy좌표 전부
        # 4방향
        for new_position in [(0, -1), (0, 1), (-1, 0), (1, 0)]:
            node_position = (currentNode.position[0] + new_position[0], currentNode.position[1] + new_position[1])

            # 범위를 넘어서는 경우
            if (node_position[0] < 0 or node_position[0] >= len(maze) or
                node_position[1] < 0 or node_position[1] >= len(maze[0]) or
                maze[node_position[0]][node_position[1]] != 0):
                continue

            child_node = Node(currentNode, node_position)
            if child_node in closedList: # 이미 닫힌 노드이다
                continue
            
            child_node.g_value = currentNode.g_value + 1
            child_node.h_value = heuristic(child_node, endNode)
            child_node.f_value = child_node.g_value + child_node.h_value

            if any(child_node == open_node and child_node.g_value > open_node.g_value for open_node in openList):
                continue

            heapq.heappush(openList, child_node)

플로이드 - 워셜 알고리듬

여태까지 본 알고리듬은 ‘단일 출발지 최단 경로’
(Single-Source Shortest Path)
‘한 노드’에서 시작해서, 다른 모든 노드로 향하는 최단 거리 찾음
(ex : 다익스트라,A*)

모든 노드 쌍에 대해 ‘최단 경로’를 찾는 문제들도 있음
APSP, All-Pairs Shortest Path

SSSP를 모든 노드에서 한번씩 돌리는 방법도 있지만
시간 복잡도가 더 든다

플로이드 워셜 : ‘모든 쌍의 최단 거리를 찾는 알고리듬 중 하나’

다익스트라와 달리 ‘인접 행렬’(2D) 사용
동적 계획법(DP) 알고리듬 (물론 ‘인접 리스트’로도 구현 가능하다)

그래프의 노드에 1~N 까지 번호를 매긴다
sp(i,j,k)를 다음과 같이 정의

i -> j의 최단 경로
중간에 1~k 노드를 거처도 됨(=k+1~n 노드는 거치지 않음)
=>1~k 노드를 거쳐가는 경우까지 고려할 때,
i->j의 최단 경로를 구하는 알고리즘
DP로 풀 수 있는 이유?

요점은 ‘최적 부분 구조’를 가지고 있으며
(각 노드에서 다른 노드로 가는 것은 ‘지역적’이며,
이를 합쳐 ‘전체적’ 해법을 구할 수 있음)
각각의 하위 문제는 ‘종속적’이다
(i->j 로 가는 과정 중, i->k로 가는 최소경로가
i-> l 로 가는 과정에 다시 이용이 가능)

플로이드 - 워셜 알고리즘의 이해

sp(i,j,k-1) : 1~ k-1 노드를 거치는 i->j 최단 거리
sp(i,j,k) : 위 공식에 ‘추가적’으로 k노드도 거치는 것을 고려

더 짧은 거리를 못 찾음(= 기존 경로를 그대로 이용)
sp(i,j,k) = sp(i,j,k-1)
더 짧은 거리를 찾음(=k 를 따라 이동해야 함)
sp(i,j,k) = sp(i,k,k-1) + sp(k,j,k-1)
=> sp(i,j,k) = min(sp(i,j,k-1),sp(i,k,k-1) + sp(k,j,k-1))

플로이드 - 워셜 복잡도

시간 복잡도: 2D 배열을 훑어야 함(O(N^2))
k마다 배열을 훑음 (O(N))
=> O(N^3)
공간 복잡도: 사용하는건 2D 배열이 전부(O(N^2))

예시 코드(Python)

import sys
import math

# '거쳐가는 정점을 기준으로'
# start -> to 의 비용과
# start -> via + via -> to 의 비용을 비교
# via에 해당하는 것을 '모든 정점'에 대하여 실행
# 이 방식으로 특정한 정점1 -> 특정한 정점2
# 에 대한 최솟값을 저장함

# 인접 행렬 방식을 사용
nNum = 4
Graph = [
    [0,5,math.inf,8],
    [7,0,9,math.inf],
    [2,math.inf,0,4],
    [math.inf,math.inf,3,0]]


def floyd_Warshall(graph,grapgSize):
    distance = [[[math.inf] for i in range(nNum)]for j in range(nNum)]

    for i in range(grapgSize):
        for j in range(grapgSize):
            distance[i][j] = graph[i][j]
    
    # k : 거쳐가는 노드
    for k in range(grapgSize):
        # i : 시작 노드
        for i in range(grapgSize):
            # j : 도착 노드
            for j in range(grapgSize):
                if distance[i][k] + distance[k][j] < distance[i][j]:
                    distance[i][j] = distance[i][k] + distance[k][j]
                
    for i in range(grapgSize):
        for j in range(grapgSize):
            print(f'{distance[i][j]:3}',end='')
        print()

floyd_Warshall(Graph,nNum)

Twitter Facebook LinkedIn

Hyun JaeHoon