트리
트리
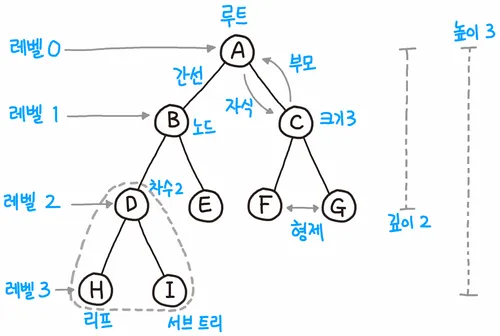
나무(tree)처럼 ‘계층적 구조’를 표현
트리 관련 용어 정리
노드(Node) : 실제로 저장하는 데이터
루트(root) 노드 : 최상위에 위치한 데이터
(시작노드, 모든 노드와 직간접적으로 연결)
리트(lefat) 노드 : 마지막에 위치한 데이터들
부모 - 자식 : 연결된 노드들 간의 ‘상대적인 관계’
(보통 낮은 레벨을 가진쪽이 ‘부모’로 불림)
(자식은 많을수도, 없을수도 있음)
(다만 부모는 언제나 1)
(부모의 부모 … 이런식으로 간접적으로 연결되면
조상 이라는 표현)
(자식의 자식… 이런식이면 ‘자손’이라는 표현)
(같은 부모를 가진, 같은 레벨의 노드를 ‘형제’라고 하기도…)
깊이(depth) : 노드 -> 루트 경로의 길이
(레벨(level)이라고도 표현한다)
높이(height): 노드 -> 리프 경로의 ‘최대 길이’
(높이 개념은 보통 RB Tree 측에서 주로 사용)
하위 트리(subTree) : 어떤 노드 아래의 ‘모든 것’을
포함하는 트리
트리는 그래프에 포함되기에 그래프 용어와 겹치는 부분도
잘 보인다
트리의 저장법
트리의 속성
- 부모와 자식 모두 노드
- 부모 : 자식 = 1 : 다수
- 자식은 언제나 부모로부터 가지를 친다
=> ‘부모’가 ‘자식’을 참조하는 방식이 직관적
자식이 여러개라면 배열로 저장하며,
자식이 2개라면(이진 트리)
left와 right 만 저장하는 방식
(tmi : 자식이 하나라면 ‘연결 리스트’와 동일해진다)
트리의 용도
계층적 데이터를 표현하기에 아주 유용하다
(ex : HTML,XML 등의 문서 개체 모델의 표현)
또한 프로그래밍 언어를 표현하는 ‘추상 구문 트리’에서도
사용된다
(ex : for문 scope가 어디까지인지…)
검색 트리를 통한 효율적인 검색 알고리즘
이진 트리
트리의 특수한 형태
(가장 많이 인식하는 형태이며, 그만큼 효율적)
-
자식이 최대 둘(왼쪽/오른쪽)
이 때, 리프를 제외한 모든 자식의 차수가 0,2 이고
모든 레벨이 같다면 ‘포화 이진 트리’
레벨이 다르라면 ‘진 이진트리’ 라고 한다 -
보통 이진 탐색 트리는 ‘계층적(재귀적)’으로
이분해 나갈 때 적합하다
이분하는 기준?
그 기준에 따라 특화된 이진 트리를 만들 수 있음!
(ex : max heap, min heap)
이진 트리는 효율적인 알고리듬 고안 가능
=> BST(이진 탐색 트리)
이진 탐색 트리 (BST)
이진 트리에 이분하는 규칙을 추가한 것!
ex : ‘왼쪽 자식은 언제나 부모보다 작다’
‘오른쪽 자식은 언제나 부모이상이다’
-
- 정렬된 배열과의 비교?
- 정렬된 배열
- 이진 탐색 전에 ‘정렬’함 + 삽입/삭제 시 추가 정렬 가능
새로 추가된 데이터는 비정렬 상태
탐색 시간(정렬 후) : O(log n)
삽입 및 삭제 : O(n)
매우 간단한 구조
메모리 한 덩어리
이진 탐색 트리 - 탐색전 정렬 필요 x
데이터 추가시 이미 정렬된 위치에 추가
탐색시간 : O(log n)
평균 삽입/삭제 : O(log n)
연결 리스트 보다 복잡한 데이터 구조
여러 데이터 메모리
- 정렬된 배열과의 비교?
-
BST의 복잡도
시간 복잡도
검색, 삽입,삭제 (평균) : O (log n)
검색, 삽입,삭제 (최악) : O (n)
공간 복잡도
O(n)-
BST의 탐색
탐색 방식은 기본적으로는 ‘이진 탐색’과 동일한 개념
(분할 정복 - 재귀적)
아래 두 노드마다 ‘하위 트리’로 이분됨
(내려갈 때마다 검색할 공간이 절반으로 줄어듦 - O(log N))다만 데이터가 하나에 ‘쏠려버린다면’
연결리스트의 ‘탐색’과 동일해지므로
O(n)이 된다 (최악)예시 탐색 코드(Python)
# 왼쪽 자식 노드에 부모보다 작은값이 있다는 조건 def SearchNode(node,data)->Node: if node == None: return None if node.data == data: return node if node.data > data: return SearchNode(node.left,data) return SearchNode(node.right,data) -
BST의 삽입
‘새로운 노드’를 조건에 맞게 받아줄 수 있는 부모를 찾음
(‘탐색’하는 것과 동일)
(찾은 후, 해당 부모의 조건에 ‘자식’이 없는지 확인
없다면 그대로 자식이 되고, 있다면 그 자식에서 다시 탐색)삽입 자체는 O(1)이지만, ‘부모’를 ‘탐색’해야 하므로
O(1) + O(log N) = O(log n)의 시간 복잡도를 가진다
예시 삽입 코드(Python)
# 왼쪽 자식 노드에 부모보다 작은값이 있다는 조건 def InsertNode(pNode,node): if pNode.data >= node.data: if pNode.right: InsertNode(pNode.right,node) else: pNode.right = node return if pNode.left: InsertNode(pNode.left,node) else: pNode.left = node-
BST의 삭제
‘리프 노드’를 지우는 것이라면 상관없지만
그 외의 경우라면,
정렬 조건에 걸맞는 위치를 가진 ‘노드’를 ‘탐색’하고
해당 노드와 값 교체
이후, 교체된 마지막 노드를 삭제
(왼쪽 자식 노드에 부모보다 작은값이 있다는 조건)
인 경우, 삭제 노드의 ‘왼쪽 노드’의 가장 오른쪽
‘자손’을 찾아 그 값과 서로 교체 후
해당 ‘자손’의 위치 노드를 삭제한다삭제 자체는 O(1)이지만, ‘값 교체 리프 노드’를 ‘탐색’해야 하므로
O(1) + O(log N) = O(log n)의 시간 복잡도를 가진다
-
중위(in), 전위(pre), 후위(post) 순회(order)
대표적인 트리의 3가지 순회법
- 요점은 왼쪽 노드 => 오른쪽 노드 의 순서 자체는 바뀌지
않으며, 현재 노드 탐색을 어느 부분에
넣느냐는 차이이다
전위 순회 : 현재 노드 -> ‘왼쪽 -> 오른쪽’
중위 순회 : ‘왼쪽 -> 현재 노드 ->오른쪽’
후위 순회 : ‘왼쪽 -> 오른쪽’ -> 현재 노드
- 각 순회법의 선택법
- 알고리즘에 따라 다르나 보통
리프보다 root를 먼저 봐야 한다면 ‘전위’
리프를 다 본 다음에 다음 노드를 봐야 한다면 ‘후위’
순서대로 봐야한다면 ‘중위’
의 방식으로 순회법을 선택한다
전위 순회 예시코드 (python)
def travelPreOrder(node):
if node == None:
return
print(node.data) # 탐색했다는 표현
travelPreOrder(node.left)
travelPreOrder(node.right)
중위 순회 예시코드 (python)
def travelInOrder(node):
if node == None:
return
travelInOrder(node.left)
print(node.data) # 탐색했다는 표현
travelInOrder(node.right)
후위 순회 예시코드 (python)
def travelPostOrder(node):
if node == None:
return
travelPostOrder(node.left)
travelPostOrder(node.right)
print(node.data) # 탐색했다는 표현
B-Tree
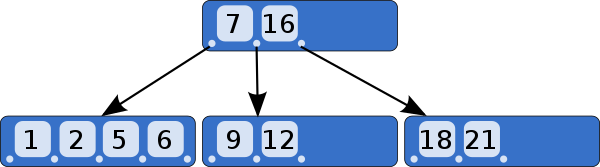
주로 ‘데이터베이스’와 ‘파일’에서 주로 사용하는
트리의 일종인 자료구조
모든 리프 노드가 같은 레벨을
가질 수 있도록 자동으로 ‘균형’(balance)을
맞춰주는 트리이다
이진 트리와 다르게 ‘하나의 노드’에 많은
데이터를 가지고 있을 수 있음
‘가지고 있는’ key의 개수 제한을 통하여
스스로 노드를 분리하는 방식을 취한다
검색 시간 복잡도는 O(log n)
-> 데이터의 효율적인 검색이 가능

댓글남기기