위상정렬

위상정렬(topological sort)

[출처] : https://m.blog.naver.com/occidere/220921661731

그래프의 노드를 선형(일직선)으로 정렬하는 방법
우선순위(방향성)은 바뀌지 않음
(A->B 의 상태라면 ‘위상정렬’ 수행 후,
B 이후 A가 나온다는 것은 없음)

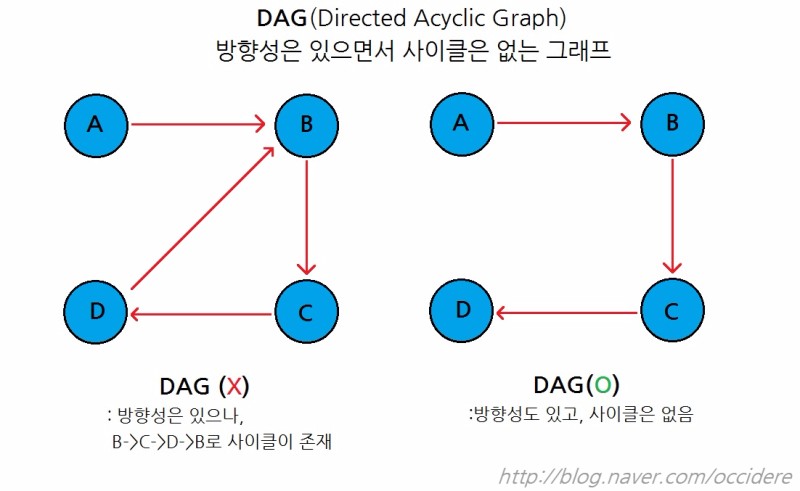
방향성, 비순환 그래프 에만 적용 가능(DAG)
-> ‘순환’하는 노드 존재시, ‘우선순위’ 판단이 불가능해진다
‘시작점’이 존재해야 한다

해답이 여럿일 수 있음

• 위상정렬인 알고리듬
  • 깊이 우선 탐색(DFS 및 DFS 응용)
  • 칸 알고리듬
    

  이러한 알고리듬은 크게 2가지 용도인데
  

  1. 실제 위상정렬을 함
  2. 위상정렬이 가능한 그래프인지 판단

위상정렬의 용도

관계에서 ‘순서’를 정하는 매우 많은 곳에 사용 가능 (프로젝트 일정 만들기,
CPU 명령어 실행 순서,
DB 테이블 로딩 순서,
순위 결정 등)

• 각 데이터 간의 ‘상대적인 순서’를 찾는 것이 목적!

위상 정렬 방법

1. 진입차수가 0인 정점을 ‘큐’에 삽입
2. 큐에서 원소를 꺼내 연결된 모든 간선을 제거
3. 간선 제거 이후에 진입차수가 0이 된 정점을 큐에 삽입
4. 큐가 빌 때까지 2~3 반복, 모든 원소를 방문하지 않았으나,
   큐가 비었다면 ‘사이클’이 존재, 모든 원소를 방문했다면,
   큐에서 꺼낸 순서가 위상정렬 결과

‘강한 결합 요소’

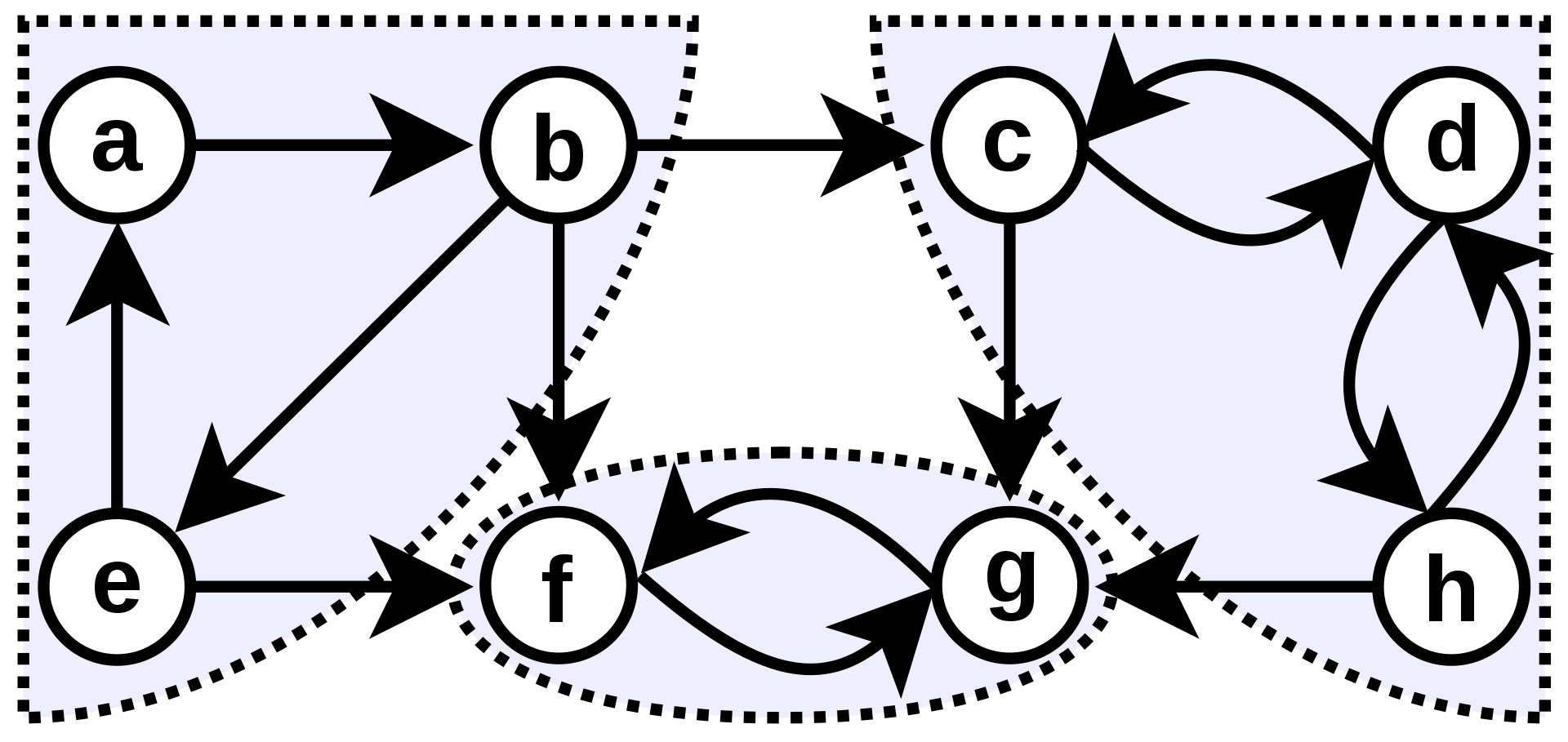
해당 ‘그래프 부분’에서 모든 노드가
직간접적으로 연결된 상태
(주로 A-> B->C->A 라면)
(A- B - C 를 하나의 ‘강한 결합 요소’라 표현가능)
(Strongly Connected Component , SCC 라 표현)

이들은 ‘방향 그래프’에서 끈끈한 관계를 가지는 노드들의
최대 그룹이며, 내부 요소들은 어떻게든 연결되어 있음

SCC는 ‘최적화’에 많이 이용
-> 해당 그룹을 ‘하나’로 볼 때, ‘위상정렬’ 알고리즘의
process 가 줄어들며, 때로는 풀기 위해 이를 이용해야할 수 있음

(위상 정렬을 하기 위해 SCC를 사용)

SCC를 판단하기 위한 알고리듬으로는

• DFS 기반 알고리듬
  • 코사라주 알고리듬
  • 타잔 알고리듬
    등이 있다
• 도달 가능성 기반 알고리듬(분할정복)

코사라주 알고리듬

SCC를 찾는 알고리즘 중 하나로서
DFS 를 두번 적용하지만, 구현하기 쉬운 알고리즘

동작 순서는 다음과 같다

1. 첫 번째 순회 (DFS)
   

   그래프를 정방향으로 순회하며,
   ‘탐색을 마친 순서’로 데이터를 저장한다
   (후위 순회 와 비슷한 매커니즘)

2. 두 번째 순회 (DFS)
   :저장한 데이터에서 ‘맨 마지막에 탐색을 마친 순서’
   부터 차례대로 역방향 DFS를 수행
   

이렇게 '탐색된 노드들'이 SCC를 이루고 있음

• 동작 원리??
  

  첫번째 DFS로 해당 그래프의 ‘노드의 연결’ 방향을 알았으며,
  두번째 DFS는 반대 순서의 정점에서 ‘자신을 가리킨 노드’
  에게 ‘자신이 가리키고 있나?’를 판별
  두번 째 DFS에서 ‘자신도 그 노드를 가리킨다면’
  ‘순회(Cycle)’ 상태이므로 SCC 상태 이며,
  이런식으로 연결되어 있는 모든 노드를 DFS로 같이
  엮어버린다
  

타잔 알고리즘

SCC를 찾는 알고리즘으로서,
DFS를 한번만 돌리는 유용한 알고리즘

동작 순서는 다음과 같다

1. DFS를 통해 그래프 탐색, 각 노드에 고유한 ID를 할당하고
   노드를 방문한 순서대로 스택에 쌓는다
2. SCC를 식별하기 위해 노드의 ID 번호와 ‘연결 가능한
   최저 번호’(low-link number)를 사용한다
   Scc 내의 노드들은 동일한 연결 가능한 최저 번호를 가짐
3. 노드를 스택에서 빼낼 때, ‘해당 노드’의 SCC를 찾는다
   속한 노드들을 스택에서 모두 제거하고, 같은 SCC로 묶는다
   
4. 모든 노드를 방문하며, SCC를 식별할때까지 반복