DP, Greedy

최적 부분 구조 (Optimal Substructure)

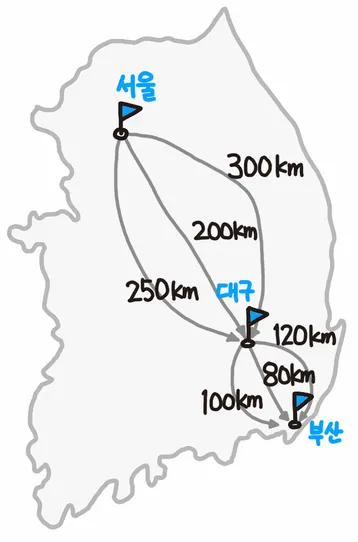
각 부분 문제의 ‘최적해’로 전체 문제의 ‘최적해’를
쉽게 얻어낼 수 있는 경우 ‘최적 부분 구조’의 조건을 성립한다고
말할 수 있다!

분할 정복, 동적 계획법을 사용하려면 문제가 ‘최적 부분 구조’ 인지 확인해야 하며
‘탐욕(Greedy)’ 알고리즘의 경우는 이 조건에 ‘탐욕 선택 속성’ 또한 만족해야
사용이 가능하다

동적 계획 (Dynamic Programming)

큰 문제를 작은 문제로 나누어 해결하는 기법

‘최적 부분 구조’를 가지고 있어야 하며
중복되는 계산은 최대한 피하는 것으로 효율성을 높인다

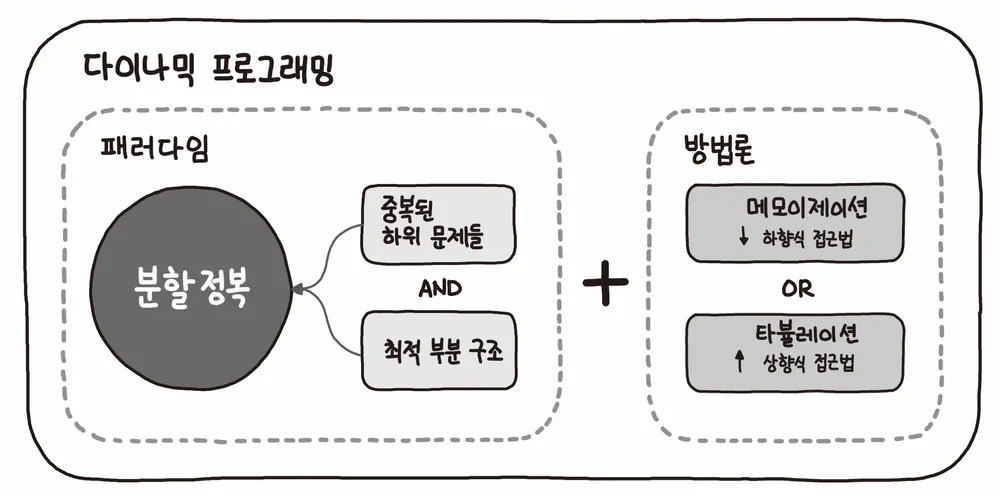
‘분할 정복’의 패러다임을 사용하며,
‘중복 계산’을 피하기 위한 ‘메모이제이션(top-down)’ 혹은
‘타뷸레이션(bottom-up)’을 사용할 수 있는 경우를 ‘DP’로 분류한다

두 기법의 차이를 조금 더 정확히 표현하자면,
‘하위 문제’의 ‘독립성’이라 말할 수 있을 것 같다

DP는 ‘하위 문제’ 간 서로 ‘종속성’이 존재하여,
종속성이 있는 문제라면, 그 문제를 해결함으로
해법을 재활용하여 ‘중복 계산’을 피할 수 있다

반면, ‘분할 정복’은 해당하는 ‘하위 문제’가 서로
‘독립적’이며, 이에 따라 각각의 해법을 낸 후
병합하는 과정을 거친다

• DP를 적용할 수 있는 문제의 특징
  

  최적 부분 구조를 ‘적용’ 가능,
  ‘하위 문제의 반복’
  (DP는 똑같은 평가방식을 적용하여 ‘다음’ 문제를 효율적으로
  풀 수 있기에 ‘하위 문제’가 많을 수록 다른 알고리즘보다 효율적)

• top - down 계획법
  

  ‘하향식’ 이란 표현으로도 소개되며,
  기존의 ‘재귀’ 함수와 비슷한 로직으로 구현이 가능하다
  아이디어 를 생각하기 쉬우며, 구현이 bottom-up보다 쉽다
  

• bottom - up 계획법
  

  ‘상향식’이란 표현을 사용하며,
  문제를 잘 분석하여 ‘최적의 순서’로 풀어나가는 방식이다
  for 문 및 반복문으로 대체되기도 하며,
  top-down 방식보다 조금 더 빠른 편이다
  
  

  ex) : fibonachi(6)을 호출한다면,
  top - down은 fibo(6)부터 호출하며,
  fibo(4) 와 fibo(5)를 호출해나가는 방식이고,
  bottom -up 은 fibo(0) 부터 시작해나가는 방식이다
  
  

  top-down 방식의 경우 이미 memory에 fibo(4)가 들어간 만큼
  ‘바로 나온다’ 하더라도 함수 호출 자체는 ‘중복’이 될 수 있다
  
  

  (물론 모든 ‘하위’ 문제를 평가할 필요가 없다면
  top-down의 성능이 더 좋을때도 있으니 case by case)

• 예시코드(Python) : 백준 2748
  

import sys

 # dp (bottom - up)
 # 데이터를 저장해 나가며
 # 기존 데이터를 이용한 방식이다
 # for 를 사용하면 이러한 접근이라 해석하기도...

maxInputCount = 91

def finboFunc(n:int)->int:
    dp = [0] * maxInputCount
    dp[1] = 1
    for i in range(2,n + 1):
        dp[i] = dp[i-1] + dp[i-2]
    
    return dp[n]

num = int(sys.stdin.readline().strip())

print(finboFunc(num))

탐욕 (Greedy)

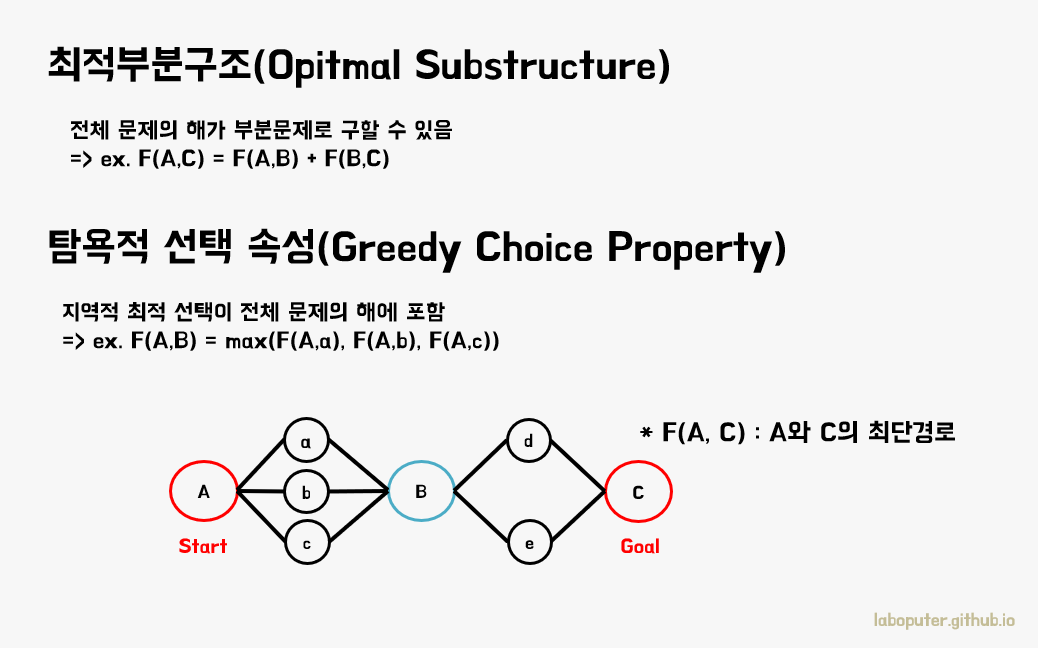
매순간 가장 좋은 선택 (지역적 최적해)을 선택하는 것이
전체적 최적해가 되는 기법

일단 작은 문제로 ‘분할’이 가능해야 한다는 점에서
‘최적부분구조’를 지녀야 하며
그러한 ‘작은 문제’에서
‘최선의 선택’을 했을 때, ‘전체적 최적해’가 된다는 ‘보장’이 있어야
탐욕 알고리즘을 사용 가능하다

그리디 알고리즘을 사용하려면,
두 가지 속성을 만족해야 하는데
이는 각각
‘최적 부분 구조’ : ‘큰 문제’의 해를 ‘작은 하위 문제’의 ‘해’로 나눌 수 있음
‘탐욕적 선택 속성’ : 지역적 최적해가 전체적 최적해
(‘탐욕적 선택 속성’은 ‘최적 부분 구조’가 존재해야 판단이 가능
그렇기에 ‘팀욕적 선택 속성’만 가져다 사용할 수는 없다)
=> ‘조건’이 주어지며, 그 조건에 맞는 ‘선택’을 우선적으로
반복해 나가는 것

• 그리디 알고리즘의 장점
  

  직관적이기에 ‘빠른 구현’이 가능하다
  ‘근삿값’을 ‘빠르게’ 반환한다
  

• 그리디 알고리즘의 단점
  

  반환하는 값이 ‘최적해’라는 보장이 없다
  => 그렇기에 ‘근사해’가 빠르게 필요하거나,
  반환값이 ‘최적해’라는 보장이 있는 경우에 주로 사용한다

• 그리디 접근 방식으로 풀 수 있는 문제
  
  • 인터벌 파티셔닝(interval partitioning)<hr>
  • 지역 시간 최소화(Minimizing Lateness)
  • 다익스트라의 최단 경로
  • k-센터 문제
  • 결정 트리 학습법
  • 허프만 코딩
  • 등등…
    => 보통 ‘최소화’,’최대화’와 관련된 문제이라면 고려
    (Greedy는 ‘최적해’를 낸다는 보장이 없기에
    문제의 세부적인 접근과 제약에 따라 다를 수 있다는 점도 유의)
• 예시코드(Python) : 백준 11047
  

import sys

 # A1 = 1, i ≥ 2인 경우에 Ai는 Ai-1의 배수
 # 해당 조건에 따라서
 # 탐욕 선택 속성 에 만족한다 판단
 # k는 1보다 크며
 # 또한 Ai 들은 전부 그 이전 값의 '배수'이다
 # 따라서 내림차순 '정렬'한 후, 해당 알고리즘이 적용 가능하다

inp = sys.stdin.readline

n,k = map(int,inp().split())

coins = [0] * n

for i in range(n):
    coins[i] = int(inp().strip())

coins.reverse()

count = 0
index = 0

while k > 0:
    if k >= coins[index]:
        share = int(k // coins[index])
        count += share
        k -= coins[index] * share
    
    index += 1

print(count)