Knapsack Problem

배낭 문제 (Knapsack Problem)

한정된 용량에 일정한 ‘가치’와 ‘용량’을 가지는 물건을 넣어
가치가 ‘최대’가 되도록 배낭을 채우는 문제

여러 변형이 존재하지만 크게 2가지 유형으로 볼 수 있다

1. 0/1 배낭 문제
   

   ‘물건’은 배낭에 ‘넣거나 넣지 않거나’만 선택 가능
   해당 문제는 ‘DP’로 풀 수 있다
   (이 경우의 시간 복잡도는 O(n^2)
   정확히는 배낭과 물건의 곱이다)

2. 분할 가능 배낭 문제 (Fractional Knapsack)
   

   물건의 ‘일부’를 잘라 배낭에 넣을 수 있는 문제
   해당 문제는 ‘그리디’ 방식으로 풀 수 있다
   (이 경우의 시간 복잡도는 O(n logN)이며
   ‘용량 대비 가치’로 물건을 선택(정렬)하기에 logN의 시간복잡도가
   필요하다)

일반적인 방법으로 푼다면 O(2^n)의 시간복잡도를 가지기에
문제의 유형에 따라서 필요한 알고리즘을 선택해서 푼다

0/1 배낭 문제의 해법

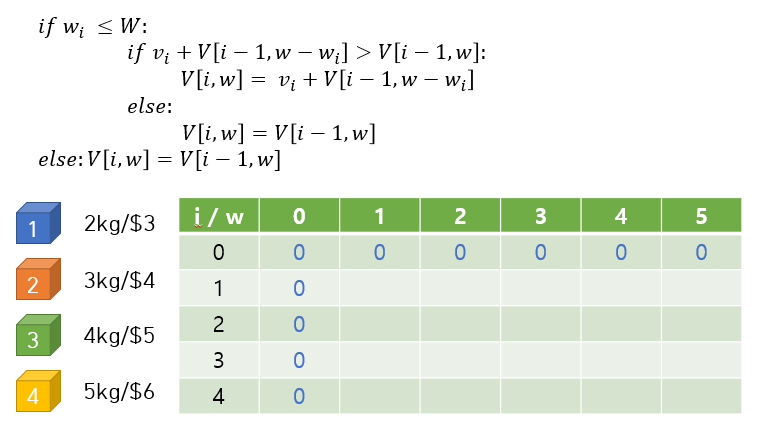
[출처] : https://gsmesie692.tistory.com/113

가치 테이블 P가 있다고 가정하고
보석의 인덱스를 i,
현재 배낭의 무게를 w로 한다면

1. i 보석을 집어넣을 때,
   그 무게(wi)가 배낭을 넘는다면, 이전 값을 넣는다
   p[i,w] = p[i-1,w]
2. 그렇지 않다면, 이전값과 p[i-1,w-wi]의 값과 비교(이전 단계의, 해당 무게를 제한 가치)
   둘 중 높은 가치를 가진쪽을 p[i,w]에 넣어준다
   p[i-w] = max(vi + p[i-1,w-wi], p[i-1,w])

해당 방식을 이용하여 ‘상향식(bottim - up)’ DP 방식으로
0/1 배낭 문제를 해결 할 수 있다!

Fracional 배낭 문제의 해법

각 항목의 ‘가치 대 용량’ 비율을 계산하고,
해당 비율이 높은 순으로 먼저 ‘가방’에 넣는다

해당 방식을 반복함으로 해결할 수 있으며
이는 ‘탐욕적 선택 속성’을 만족하기에
‘그리디(탐욕)’ 접근법으로 해결이 가능하다

• ‘탐욕적 선택 속성’을 가지고 있다 할 수 있는 이유?
  
  1. 각 항목은 ‘가치’와 ‘용량’을 가지고 있음
  2. 항목을 ‘분할’할 수 있음
     => 따라서 ‘가치 대 용량’ 비율 이라는 ‘지역적 최적해’가 존재
     또한, 이러한 ‘지역적 최적해’를 선택하는 것이
     ‘전체적 최적해’라는 점의 증명은 아래와 같다
     
     • X가 가장 ‘가치 대 용량’ 비율이 높으나, 이를
       완전히 선택하지 않고 다른 항목으로 채운다 가정한다면,
       X를 우선적으로 채운 가방의 가치 >
       X를 우선적으로 채우지 않은 가방의 가치
       
     • 결국 ‘주어진 용량’ 안에 ‘가장 가치가 높은 물건’을 담는
       것이 문제의 최적해 이기에
       ‘탐욕’적으로 선택하여도 ‘전체적 최적해’가 보장이 되는 상황이다

이해에 도움이 된 사이트

• https://gsmesie692.tistory.com/113